Abstract
Objectives:
Research questions about how and why health trends differ between populations require decisions about data analytic procedure. The objective was to document and compare the information returned from stratified, fixed effect and random effect approaches to data modelling for two prototypical descriptive research questions about comparative trends in toothbrushing.
Methods:
Data included five cycles of the Health Behaviour in School-aged Children 2006 to 2022, which provided a sample of 980192 11- to 15- year olds from 35 countries. Using logistic regression models and generalized linear mixed models, toothbrushing daily was regressed on time, following the three approaches to analysis of trends.
Results:
The stratified approach suggested a positive but non-linear trend in toothbrushing from 2006 to 2022 in most countries but provided no statistical inference on the variation. The fixed effect and the random effect approach converged on a positive but flattening overall trend, with a statistically significant country variation in trends.
Conclusion:
Only the fixed effect approach and the random effects approach provided clear answers to the research question. Additional methodological considerations for making an informed choice of analytical approach are discussed.
Introduction
In the dynamic landscape of public health, staying abreast of emerging trends in health and health behaviours is paramount for effective policy formulation and implementation. Health trends, characterized by developments in risk behaviours by socio-demographic factors, serve as invaluable indicators of the evolving public health policy, and has received increasing attention as a field of research [1–6].
Adopting a comparative perspective on time trends enables interesting research questions about how and why health trends differ between populations. Such research questions also set strong requirements for study design, measurement, model specification, and choice of data analytic procedure. The “Health Behaviour in School-aged Children study (HBSC)” has a research design that is highly relevant for research questions about time trends in health. In the HBSC study, survey data collection is repeated every 4 years, on independent samples of new cohorts of 11– to 15–years olds from the same countries or regions. The study has a repeated structure at the country/region-level with country A, B, and C measured at several time points, but a cross-sectional structure at the individual-level. This design allows for tests about how societies change, but not how individuals change.
Previous methodological papers have addressed the unique challenges related to obtaining comparability of research protocols, sampling frames, and measurement [7–9], but the required data analytic decisions have received less attention. The current study highlights the choice of analytic approach in empirical analyses of comparative trends.
The generic class of regression models provide a flexible analytical framework for comparative time trend analysis. In such models, a health outcome is the dependent variable for the independent variable historical time. For a simple linear model, the trend can be summarised through a single parameter: the regression coefficient of change per time unit.
Trends are not always linear, and specification of the shape of the trend is a central task in comparative trend analysis. When there are three or more cycles of data, non-linear time trends can be fitted through higher-order polynomials, including quadratic and cubic terms of time. A simple linear shape makes a direct interpretation possible, where the trend can be translated into an “increase” or “decrease” over time. When the model include quadratic and cubic effects, the trend is a composite of effects, and difficult to interpret directly form the regression model coefficients. To interpret non-linear trends, obtained model predictions can provide the necessary information.
A challenge particular to comparative time trend studies is how to model and test country differences of trends. By focussing on regression model-based tests of trends, we have identified three major comparative approaches: the stratified approach, the fixed effect approach, and the random effects approach to trends.
The stratified approach involves running a series of regression analyses split by country, regressing the relevant health outcome with time as the focal independent variable. A common model is specified and repeated for each country. With a dichotomous health outcome as dependent variable and time as continuous independent variable the generalized linear regression model for binomial data with a logit link becomes:
In the fixed effect approach, the average trends and country differences of trends can be modelled through specification of main and interaction effects of time and country, where the effect of country is specified through, for example, deviation coding or simple contrast coding. With a simple contrast specification for countries A,B,C this generalized linear model becomes:where and time describe the intercept and effect of time for the reference country A, and describe country B and C differences in intercept relative to country A, and and are interaction terms describing country B and C difference in the effect of time relative to country A.
In the random effects approach, the average trend is modelled as a fixed term (), but the country differences in such trends are parameterized through random variance components that can be functions of time. The random effects can be structured in several ways [10]. The “societal growth curve specification” is relevant for our purpose [10]. For a comparative repeated cross-sectional study, a three-level generalized linear mixed model can be specified, using person (i), country-year (j) and country (k) as levels within the model:
This three-level composite specification includes a fixed part intercept , a fixed effect of time , and a random part with three components: A random country-year-level (j) intercept component capturing fluctuations within country across years; a random country-level (k) intercept component capturing country-level differences in the dependent variable, and a country-level random slope component capturing between-country variation in the slope of time.
The Current Study
With a considerable diversity in types of research questions and available analytical approaches, there is a need to examine the relative utility and relevance of different approaches to comparative time trend analyses in applied research.
In the current study, we demonstrate and compare model information and results from stratified, fixed effect and random effect approaches to comparative trends on a real-data case from the HBSC study: adolescent toothbrushing between 2006 and 2022 in 35 countries. The used data partly overlap with a previous study of trends in toothbrushing [11], but in the current study the primary objective is methodological.
To structure the comparison between approaches, we used each approach to answer two seemingly simple research questions:
Research question 1 (RQ1): Did toothbrushing show an overall linear time trend 2006–2022?
Research question 2 (RQ2): Did countries/regions show different time trends?
Methods
Data
The Health Behaviour in School-aged Children study is a large WHO-collaborative school-based survey carried out every 4 years, among a sample of 11-, 13-, and 15-year-olds, with an even distribution of boys and girls. Respondents completed anonymous questionnaires in a class-room setting following a standardized protocol, which has been developed and updated for every survey round. The HBSC protocol is used across all participating countries, ensuring high comparability of data across an increasing number of countries over time and repeated survey rounds. In the current study only data from five of the total 11 cycles of data collection was used, covering the period 2006 to 2022. Open data can be accessed on https://www.uib.no/en/hbscdata/113290/open-access. Countries or regions that took part in all five survey rounds were included, representing a sample of N = 980,192 students from 35 countries or regions, with 50.6% girls, and balanced age category composition. The 35 countries and regions are listed in Table 1.
TABLE 1
| Country/region | No | Yes | % |
|---|---|---|---|
| Austria | 5,445 | 17,002 | 75.7 |
| Belgium (VLG) | 9,687 | 16,279 | 62.7 |
| Belgium (WAL) | 9,706 | 15,763 | 61.7 |
| Canada | 19,903 | 39,899 | 68.4 |
| Croatia | 10,052 | 16,910 | 62.7 |
| Czech Republic | 10,331 | 28,274 | 73.3 |
| Denmark | 4,872 | 17,351 | 78.1 |
| Estonia | 7,985 | 14,193 | 64.0 |
| Finland | 10,468 | 13,915 | 57.0 |
| France | 8,978 | 24,151 | 72.8 |
| Germany | 6,034 | 22,385 | 78.7 |
| Greece | 11,214 | 11,589 | 50.8 |
| Greenland | 2,352 | 3,425 | 59.3 |
| Hungary | 8,073 | 11,838 | 59.4 |
| Iceland | 15,202 | 32,441 | 68.1 |
| Ireland | 7,008 | 13,990 | 66.6 |
| Israel | 6,955 | 13,564 | 66.9 |
| Italy | 5,620 | 15,886 | 73.9 |
| Latvia | 11,445 | 12,814 | 52.8 |
| Lithuania | 12,774 | 12,523 | 49.5 |
| Luxembourg | 5,855 | 14,223 | 70.8 |
| Netherlands | 4,891 | 17,219 | 77.7 |
| Norway | 4,566 | 13,794 | 75.1 |
| Poland | 8,500 | 16,304 | 65.7 |
| Portugal | 7,498 | 16,403 | 68.6 |
| Romania | 13,358 | 13,087 | 49.5 |
| Slovakia | 9,820 | 15,515 | 61.2 |
| Slovenia | 8,835 | 18,614 | 67.5 |
| Spain | 11,630 | 21,395 | 64.2 |
| Sweden | 4,763 | 22,334 | 82.4 |
| Switzerland | 5,011 | 27,152 | 84.4 |
| North Macedonia | 8,115 | 13,947 | 63.2 |
| England | 4,813 | 16,077 | 76.7 |
| Scotland | 7,111 | 20,964 | 74.6 |
| Wales | 18,452 | 47,152 | 71.8 |
| Total | 307,322 | 648,372 | 67.9 |
Sample frequency of toothbrushing twice or more daily in 35 countries and regions in five cycles of the Health Behaviour in School-aged Children study (2006–2022).
Measures
Toothbrushing was measured with a single frequency item: “How often do you brush your teeth?” with the five response categories (1: “More than once a day”; 2: “Once a day”; 3: “At least once a week but not daily,” 4: “Less than once a week” and 5: “Never”). In the analyses for the present paper the outcome was defined as “toothbrushing more than once a day,” collapsing the four other categories to 0.
Data Analysis
We used R version 4.4.1 [12] for all statistical analysis and visualization, R stats glm function for the stratified approach and the fixed effect approach, and the lme4 [13] package glmer function for the random effects approach. Model selection was based on Likelihood ratio test (LRT) of nested models and Akaike’s information criterion (AIC) and Bayes information criterion (BIC). Model assumptions for the logistic regression models include no outliers, inclusion of all relevant independent variables, linearity across the prediction, and independence of responses. The logistic regression model with random effects also assumes normal distributed random effects.
We tested logistic regression model assumptions through the random quantile residual function of the STATMOD R package [14]. As compared to Pearsons or Deviance residuals, random quantile residuals are less affected by the scaling of the dependent variable and improves the diagnostic information from analysis of residuals from discrete outcomes [15]. For the random effect approach, we also examined the assumption of normal distributed random effects with normal QQ-plots.
For the stratified approach we used the generalized linear model for binomial data, with a logit link function, also referred to as a logistic regression model. For each region, we regressed the dependent variable toothbrushing on continuous time. Linear (M1), quadratic (M2) and cubic (M3) effects of time was entered blockwise, with one set of analyses per country or region. In all analyses, time was centred at year 2014, to reduce multicollinearity between time, time quadratic, and time cubic. Centred time was rescaled to 10-year unit, making the regression coefficient the change in toothbrushing per 10-year period.
For the fixed effect approach, we modelled the average trends and country/region differences through specification of main and interaction effects of time and country/region, using deviation contrasts for country/region. Model M0 included main effects of country/region. Models M1 to M3 included linear, quadratic and cubic effects of time. To test country/region differences in trends (RQ2) we entered country/region by time, country/region by quadratic time, and country/region by cubic time (M4 to M6). Likelihood ratio test of the main effects of time allowed for the assessment of the statistical significance of an overall trend across all countries (RQ1), while the interaction time by country allow for at omnibus test of region differences in trends (RQ2).
The random effects approach was implemented through a three-level generalized linear mixed regression model including a constant logistic conditional variance at the student level (), and random effects at the region-year and region level. Model M0 was a null model including a fixed intercept () and random country/region-year and country/region intercept variance components. Models M1 to M3 tested fixed linear (), quadratic () and cubic time (), relevant to interpret the trend shape, and the overall average trends of toothbrushing (RQ1). Model M4 included a random slope of time at the region level , relevant to our research question about between-region differences in trends in toothbrushing (RQ2). R glmer function uses Laplace approximation when there are multiple levels of random effects. We extracted model-based predictions with the ggeffects package [16]. Assumptions of normal-distributed random effects were examined with diagnostic QQ-plot from sjPlot [17] package.
Results
Table 1 shows the sample frequency of toothbrushing twice or more often daily per country or region, collapsed over study cycles.
Stratified Approach
Prior to statistical analysis we inspected the descriptive frequencies of toothbrushing per country and region over time, as shown in Supplementary Figure S1. We note different patterns across countries.
Supplementary Table S1 shows the results of 35 blockwise logistic regression models with toothbrushing as the dependent variable regressed on time, time-quadratic and time-cubic in the stratified approach, with three model blocks (models M1 to M3) per country/region. Supplementary Table S2 shows the model summary statistics Deviance, BIC, AIC and LRT model comparisons for the 35 sets of analyses.
Model diagnostics of quantile residuals for model M3 in the stratified approach revealed no patterns with the linear predictor (Supplementary Figure S2), and the normal QQ plot suggested no residual deviation for any country/region (Supplementary Figure S3).
The LRT difference between models informs about the shape and magnitude of trends, and post hoc we used the information to summarize different trend patterns. The profile of trends in the stratified approach is shown in Figures 1A–F. For two countries there were no statistically significant trends (Austria, Netherlands). Four countries (panel B) showed linear trends only (Estonia, Croatia, Hungary, Sweden). For eight countries (Finland, England, Ireland Iceland, Luxembourg, Latvia, Slovenia, and Slovakia) there were statistically significant linear and quadratic blocks (panel C), and for twelve countries blocks of linear, quadratic and cubic components were all statistically significant [panel D: Belgium (VLG), Canada, Switzerland, Czech Republic, Spain, France, Scotland, Greenland, Lithuania, North Macedonia, Portugal, Romania]. Six countries (panel E) showed a pattern of statistically significant linear effects, non-significant quadratic effects, and significant cubic effects [Belgium (WAL), Denmark, Greece, Israel, Italy and Norway]. Three countries (panel F) showed a pattern with significant blocks of quadratic and cubic terms but without a significant linear block (Wales, Poland and Germany).
FIGURE 1
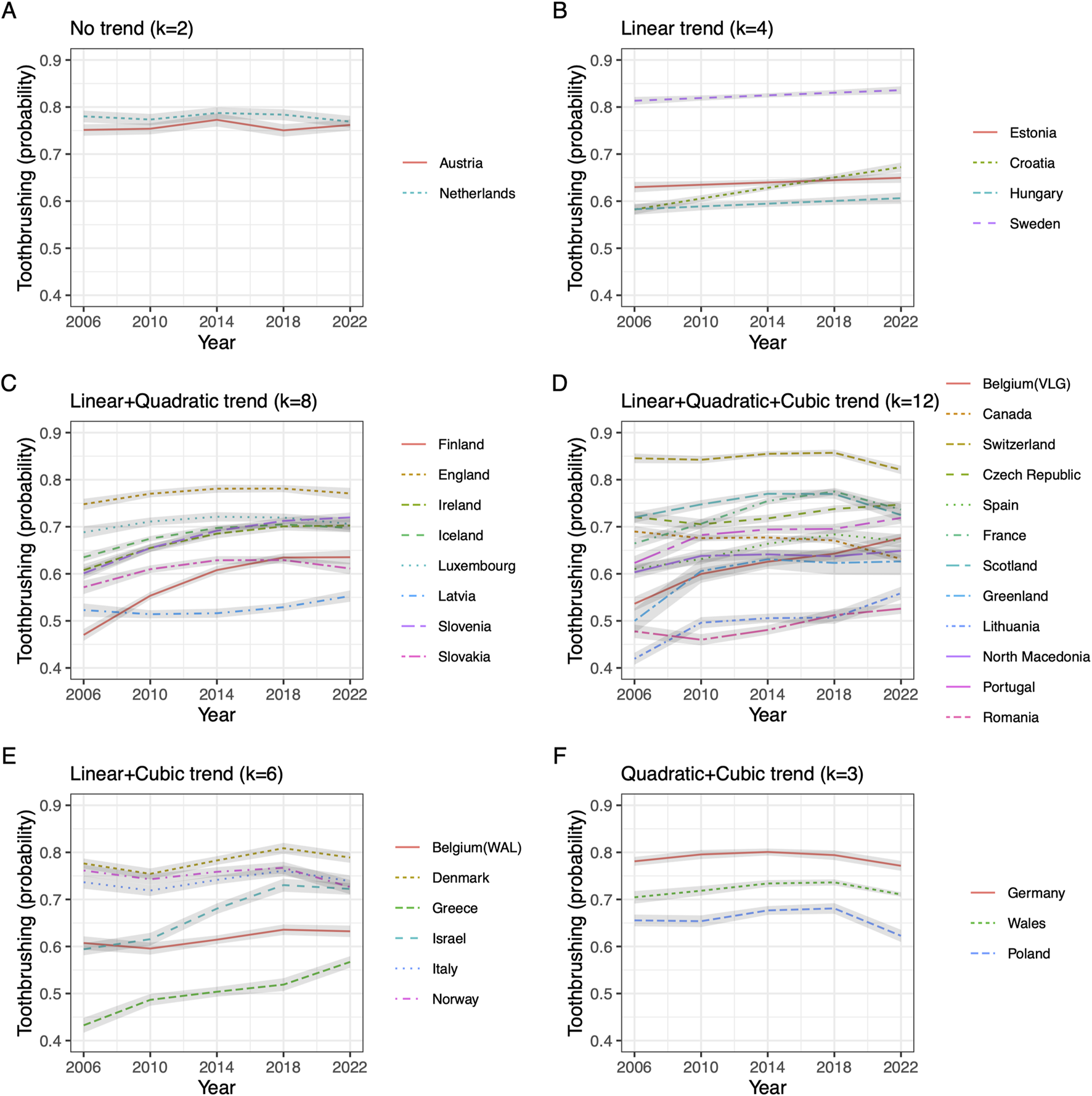
Predicted toothbrushing by time per pattern of trend components, stratified approach. (A) Countries with no trend; (B) Countries with linear trend; (C) Countries with linear and quadratic components; (D) Countries with Linear, quadratic and cubic trend components; (E) Countries with linear and cubic trend components; (F) Countries with quadratic and cubic trend components (Data from Health behaviour in school-aged children 2006–2022).
To summarize, the stratified approach showed a strong diversity of trend shape, with few countries showing a monotone linear trend, but most countries showed a composite positive trend in toothbrushing.
Fixed Effect Approach
Table 2 shows the model summary for the fixed effect approach. The likelihood ratio test of the difference between nested models revealed statistically significant increments in model fit for linear time (M1), quadratic time (M2) and cubic time (M3), as well as interactions country/region by linear time (M4), country/region by quadratic time (M5), and country/region by cubic time (M6). AIC and the LRT suggested M6 to be the best model, whereas BIC identified model M4 as the best fitting model. The results of model M6 of the fixed effect approach suggested a linear, quadratic and cubic component in the overall trends, and that linear, quadratic and cubic components were different across countries and regions.
TABLE 2
| M0 No trend Country/Region main effects |
M1 Linear Country/Region main effects |
M2 Quadratic Country/Region main effects |
M3 Cubic Country/Region main effects |
M4 Linear by Country/Region |
M5 Quadratic by Country/Region |
M6 Cubic by Country/Region |
|
|---|---|---|---|---|---|---|---|
| Parameters | 35 | 36 | 37 | 38 | 72 | 106 | 140 |
| AIC | 1,167,721.99 | 1,166,648.29 | 1,166,370.11 | 1,166,358.81 | 1,165,122.03 | 1,164,902.00 | 1,164,752.77 |
| BIC | 1,168,133.94 | 1,167,072.01 | 1,166,805.60 | 1,166,806.08 | 1,165,969.48 | 1,166,149.64 | 1,166,400.60 |
| Deviance | 1,167,651.99 | 1,166,576.29 | 1,166,296.11 | 1,166,282.81 | 1,164,978.03 | 1,164,690.00 | 1,164,472.77 |
| df.residual | 955,659 | 955,658 | 955,657 | 955,656 | 955,622 | 955,588 | 955,554 |
| LRT | 32,789.16 | 1,075.70 | 280.18 | 13.30 | 1,304.78 | 288.03 | 217.23 |
| df Mk–Mk.1 | 34 | 1 | 1 | 1 | 34 | 34 | 34 |
| p-value | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 |
Model summary for fixed effects approach. Model comparisons are conducted on likelihood ratio test (LRT) difference test on model difference degrees of freedom, Akaike’s information criterion (AIC) and Bayes information criterion (BIC) (smaller is better). (Health behaviour in school-aged children 2006–2022).
Note. Null deviance is 1,200,441.1, df = 955,693.
Supplementary Figure S4 include model diagnostics for model M6 fixed effect approach. The quantile residuals for model M6 were constant across the linear prediction (panel A). Residuals did not vary as a function of time (panel B) or country/region (panel C). The quantile-quantile plot (panel D) suggested that there were no outlying cases.
Supplementary Table S3 shows the model coefficients for model M6 for the fixed effect approach. As the trend has three components the single regression coefficients convey limited information about the total trend for a country or region. The model coefficients for time show that at time 0 the mean linear growth rate per decade is 0.19, but the negative quadratic effect of −0.13 and cubic effect of −0.10 indicate that the average growth rate changed across time, levelling off over time. This indicate that the overall trend was non-linear.
The deviation contrasts for the main effect, represent each country/regions difference to the mean level of toothbrushing at time 0 (in our example: 2014), here in logit unit. The B/SE ratio for each deviation contrast is the test statistic for the hypothesis that the specific country/region contrast is different from the mean intercept, or from the mean linear component, the mean quadratic component or the mean cubic component.
More specific information about the trends and the differences in trends for specific countries were obtained through model-based predictions and relevant linear composites, and we illustrate these predictions and the random effect predictions in the next section on random effects (Figure 2, panels A, B).
FIGURE 2
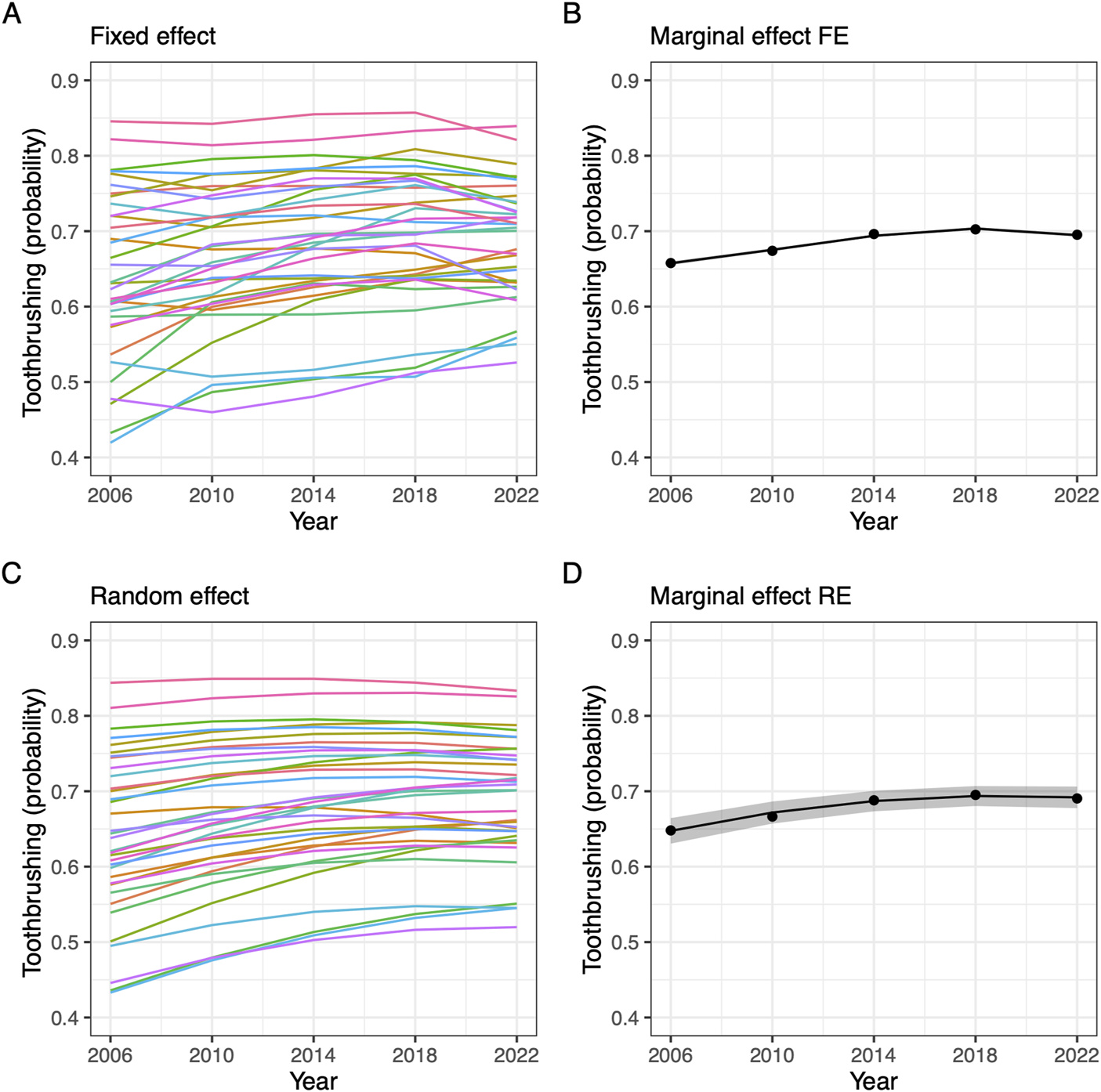
Predicted toothbrushing by time. (A, B) Show predictions from fixed effect model, (C, D) shows predictions from random effect model. (A, C) give predictions per country or region, one line per country/region. (B, D) give mean overall prediction, with confidence intervals (Data from Health behaviour in school-aged children 2006–2022).
Random Effects Approach
Table 3 shows the model summaries results from the random effects approach. The likelihood ratio test of nested model differences indicated statistically significant linear (M1) and quadratic (M2) components, but not a cubic component (M3). For model M4, the inclusion of a random slope (V1time) and a slope-intercept covariance (COV01) on two degrees of freedom led to a statistically significant better model fit, suggesting that the slope of time varied across countries. The statistical inference on the added random slope is only approximate, as we do not have a restricted maximum likelihood for the logistic mixed model. Based on these results, we tested a trimmed version of the model M4 without cubic effects, model M4b. The BIC for this model was the smallest of all models.
TABLE 3
| Statistic | M0 No trend |
M1 Linear |
M2 Quadratic |
M3 Cubic |
M4 Random slope linear |
|---|---|---|---|---|---|
| Model parameters | 3 | 4 | 5 | 6 | 8 |
| AIC | 1,165,085.51 | 1,165,032.45 | 1,165,020.26 | 1,165,020.77 | 1,164,981.43 |
| BIC | 1,165,120.82 | 1,165,079.53 | 1,165,079.11 | 1,165,091.40 | 1,165,075.59 |
| Deviance | 1,165,079.51 | 1,165,024.45 | 1,165,010.26 | 1,165,008.77 | 1,164,965.43 |
| LRT | 55.06 | 14.19 | 1.48 | 43.35 | |
| Nested model df Mk vs. Mk.1 comparison | 1 | 1 | 1 | 2 | |
| p-value | <0.001 | <0.001 | 0.224 | <0.001 |
Model summary for random effects approach. Model comparisons are conducted on likelihood ratio test (LRT) difference test on model difference degrees of freedom, Akaike’s information criterion (AIC) and Bayes information criterion (BIC) (smaller is better). (Health behaviour in school-aged children 2006–2022).
Supplementary Table S4 show model coefficients for the selected model M4b, with a fixed part and a random part. The fixed part indicated that for the average country (at random effects = 0) there was positive linear trend component = 0.134 and the negative quadratic component = −0.125 indicated that the positive trend levelled of as a function of time.
The random intercept SD (U0) = 0.079 at country/region-year level, suggested that toothbrushing fluctuate within a prediction interval + −0.079*1.96 = [−0.158 to 0.158] logit units, relative to the linear slope of a country. The random intercept SD at the region-level (V0) = 0.421 indicated that for an average country, adolescents’ prevalence of toothbrushing would fall within the 95% prediction interval [−0.02 to 1.63], which after logit transformation to probabilities implies a prevalence of “toothbrushing more than once a day” to vary between 49% and 83% at time 0 (year 2014). The random slope of linear time (V1) with an SD of 0.122, suggested that the for the population of countries the slope of the linear component would fall within −0.134+−0.122*1.96, giving a 95% prediction interval in logit units for the linear slope of linear time [−0.11, 0.37]. The negative corelation between intercept and slope means that countries with a low level of toothbrushing tended to have a stronger positive slope of time. We also computed model-based predictions for each specific country/region, relevant for specific inference about the differences in trends. A quantile-quantile plot for each random variance component indicated a close fit to a normal distribution .for both country/region and country/region-year level, as shown in Supplementary Figures S5, S6.
Figure 2 shows the model-based predicted probability of toothbrushing as a function of time for the best fitting models of the fixed effect approach and the random effect approach. The upper half of the figure shows results from the fixed effect approach model M6 (panels A and B), and the lower half shows the results for the random effects approach model M4b (panels C and D). The confidence intervals for the average trend were notably slimmer for the fixed effect approach.
The fixed effect approach and the random effect approach predicted a group of countries and regions with a higher level of toothbrushing, and no apparent trend. For the number of regions that started with a low to medium level of toothbrushing the prediction was a trend of increased toothbrushing. The average marginal effect showed that the trend is positive but flattening.
Table 4 summarises the model information and findings from the three approaches included.
TABLE 4
| Study criterion/Approach | Information/Parameters | Main findings |
|---|---|---|
| Overall trend | ||
| Stratified | Provides trends per country/region. Specific statistics on trend but no test statistic for the overall average trend | Of 35 regions. 30 regions showed a trend with a linear component, of which 27 slopes were positive. No test for overall average trend |
| Fixed effect | Test of overall average trend trends and the shape of trend, conditional on country/region differences | Statistically significant overall trend with linear, quadratic and cubic components |
| Random effect | Tests of overall trends and the shape of the trend for the average country/region | Statistically significant overall trend with linear and quadratic components |
| Trend differences | ||
| Stratified | Post hoc profiles of different trend patterns, but no test statistic for the regional differences | Different slope results for countries/regions, and different types of trends across countries/regions |
| Fixed effect | Omnibus model tests and specific test of regional differences through contrast specification. Model-based predictions for country/region | Statistically significant country/region differences in linear, quadratic and cubic components of trend Specific test of each country/region vs. average for intercept, linear, quadratic and cubic effects |
| Random effect | Omnibus model tests for random effects, model-based prediction intervals for population, and specific country/region | Statistically significant country/region differences in linear slope of time Specific predictions of country/region trend differences |
Summary of model information, and main results by data analytic approach.
Discussion
The objective of the current study was to compare the information returned from stratified, fixed effect and random effect approaches to comparative time trends in toothbrushing. The type of information and results returned from the analyses was different for the three approaches.
The stratified approach provided a high level of detail about each country/region trend, but did not provide statistical tests of direct relevance to our two research questions. To answer our research questions on the overall trend and the differences in trend we used an implicit, but non-parametric approach by counting and ranking the number of statistically significant trends, a procedure sometimes referred to as “vote counting.” Our post hoc classification of trend profiles indicated variation across countries and an overall upwards trend, but the count of profiles does not represent a statistical inference.
For the fixed effect approach and the random effects approach, our two research questions could be operationalised as testable hypothesis about model parameters, either expressed as fixed effects or as random effects. Both approaches provide omnibus tests as well as specific country-level inference about effects, and their conclusions overlapped but were not identical. For both approaches the omnibus tests concluded with a non-linear positive but gradually flattening trend in toothbrushing, and both approaches concluded with cross-national differences in the trends. The fixed effect approach included tests country/region by time, country/region by time quadratic, and country/region by time cubic, and provided a more detailed perspective of trend in each country/region. In studies of region differences in trends, region-specific conclusions are of key interest to the researcher, and the fixed effect approach can to high degree provide relevant information, however this level of specificity comes at the cost of model complexity. The most comprehensive models (M6 fixed effect approach), included 136 country/region contrasts, which at least from a practical perspective, is high.
The random effect approach did not include separate fixed estimates for the specific countries/regions, but produced country/region-specific conditional predictions. In a context with many countries and many time points, the specified random slope of time provide a flexible yet parsimonious approach to modelling cross-national differences in the trend. Compared to fixed effect approach, the results from the random effect approach suggested a simpler parametric shape for the overall time trend, as the cubic main effects (model M3) did not achieve statistical significance. The subtle differences in conclusion on the shape of the overall trend between the fixed effect approach and the random effects approach might reflect specification differences. The country/region-year random component (Uoj) models random fluctuations across time, thus reducing the need for to include fixed part non-linear components for each country. Conceptually, the provision of a random country-year component can be important, by separating longer term linear trends from short term societal changes that do not follow a parametric linear curve, and therefore might reflect different underlying societal processes.
Under the current sample size and number of countries, key model assumptions were satisfied in all three approaches. However, the model assumptions of the three approaches have different sensitivity to number of country/region units included. The stratified and fixed effects approach can be conducted with 5 countries and with 35 countries without expected violations of model assumptions. For the random effects approach random variance components and standard errors of estimates tend to be downward biased when the number of higher units is small [18, 19]. Under the current frequentist approach, 35 countries or region units is just above the recommended limit of at least 30 countries to achieve accurate estimates of the logistic mixed model [18]. If the number of country units is smaller, Bayesian computation of random country-level effects is a relevant alternative as this method has less bias in small sample situations [19], but the Bayesian computation require researchers to make additional assumptions about the prior distribution.
Limitations
We only considered polynomial specification of time. This specification may work well to capture non-linearity within a specified time frame but be less accurate in long term projections. Decisions about trend shape need to consider both the number of time points with observations and the length of the period covered. If events have occurred during the period covered, such as sudden technological innovations, macroeconomic shocks, changes in health legislation, or pandemics, a piecewise model or simple contrasts as an extension of the simple linear trend could be relevant alternative specifications to quadratic and cubic effects. In piecewise models the slope of a linear time effects can change at a given time point, allowing for an overall non-linear trend and turning points. Generalized additive models and generalized additive mixed models [20] provide a general regression framework for non-linear modelling of trends.
Secondly, omission of unmeasured time-invariant or time-varying independent variables might bias regression trend estimates. Unmeasured third variables at the country/region level might particularly affect the random effect approach to trend analysis, as the random region-level effect will include the effects of such unmeasured variables. For the fixed effect approach, conditioning on the main effect of region account for region level third-variables. The stratified approach might be least vulnerable to omission of region-level factors, as relevant third variables are restricted to those affecting the within-country context. As a basic strategy to minimize endogeneity, comparative time trend studies can counteract bias by collecting information on country/region indicators and include that information as covariates in the model.
Our comparison of approaches was conducted on a set of descriptive research questions, which represent an important first stage in trend analysis. Future research should examine how the three approaches can be extended to explanatory trend analysis with country-level moderators and mediators of comparative trends, where two-stage modelling [21] and hybrid random effects model [22] might provide relevant example starting points for a comparison.
Conclusion
We compared the model information and results obtained from stratified, fixed effect, and random effect approaches to comparative trend analyses of adolescent toothbrushing. Our case clearly demonstrated that statistical inference about average time trends and trend differences is lacking with a stratified approach. For statistical inference regarding the trend and trend differences, the fixed effect approach provided a high level of specificity. The random effects approach produced similar conclusions, but with less detail and specificity in the trend for each country.
Statements
Ethics statement
In each country the studies were conducted in accordance with the local legislation and institutional requirements for ethical approval at the time of study implementation. Participants provided informed consent for participation as per national human participant requirements.
Author contributions
All authors contributed the conceptualisation of the paper. CS initiated and drafted the first submission of the manuscript. FE, CR, and AC conducted the analysis for the first submission. TT revised the text, reanalyzed the data, and resubmitted the manuscript. All authors contributed to the article and approved the submitted version.
Funding
The author(s) declare that financial support was received for the research, authorship, and/or publication of this article. The study was supported by the project “Research of Excellence on Digital Technologies and Wellbeing CZ.02.01.01/00/22_008/0004583” which is co-financed by the European Union. The writing of the manuscript was supported by a grant from the Meltzer Research Foundation (Grant 1700-32053) to TT.
Acknowledgments
The International HBSC Coordinator was Jo Inchley (University of Glasgow, United Kingdom) for the 2018 and 2022 survey and Candace Currie (Glasgow Caledonian University, United Kingdom) for the 2006 to 2014 surveys. The Data Bank Manager was Professor Oddrun Samdal (University of Bergen). The survey data included in this study were conducted by the following principal investigators in the 35 countries: Austria (Rosemarie Felder-Puig and Wolfgang Dür), Flemish Belgium (Bart De Clercq, Maxim Dirckens, Carine Vereecken, Anne Hublet, and Lea Maes), French Belgium (Katia Castetbon and Danielle Piette), Canada (William Pickett, Wendy Craig, John Freeman), Croatia (Ivana Pavic Simetin), Czech Republic (Michal Kalman and Ladislav Csemy), Denmark (Mette Rasmussen, Pernille Due, Katrine Rich Madsen), England (Fiona Brooks, Ellen Klemera, Sally Kendall, Sabina Hulbert), Estonia (Leila Oja, Katrin Aasvee, and Mai Kaser), Finland (Jorma Tynjälä, Leena Paakkari), France (Emmanuelle Godeau), Germany (Matthias Richter, Petra Kolip, Ulrike Ravens-Sieberer, and Klaus Hurrelmann), Greece (Anna Kokkevi, Anastasios Foutiou), Greenland (Birgit Niclasen), Hungary (Ágnes Németh), Iceland (Arsaell M. Arnarsson and Thoroddur Bjarnason), Ireland (Saoirse Nic Gabhainn), Italy (Franco Cavallo, Alessio Vieno), Israel (Yossi Harel-Fisch), Latvia (Iveta Pudule), Lithuania (Kastytis Šmigelskas and Apolinaras Zaborskis), Luxembourg (Carolina Catunda, Andreas Heinz, Helmut Willems, Yolande Wagener), the Netherlands (Gonneke Stevens, Saskia van Dorsselaer, Wilma Vollebergh, and Tom de Bogt), North Macedonia (Lina Kostarova Unkovska), Norway (Oddrun Samdal, Ellen Haug), Poland (Anna Dzielska, Joanna Mazur and Barbara Woynarowska), Portugal (Margarida Gaspar de Matos and Tania Gaspar), Romania (Adriana Baban and Diana Taut), Scotland (Jo Inchley and Candace Currie), Slovenia (Helena Jericek and Eva Stergar), Slovakia (Andrea Madarasova Geckova), Spain (Carmen Moreno), Sweden (Petra Löfstedt, Lilly Augustine, and Ulla Marklund), Switzerland (Marina Delgrande-Jordan, Hervé Kuendig, Emmanuel Kuntsche), Wales (Chris Roberts).
Conflict of interest
The authors declare that they do not have any conflicts of interest.
Supplementary material
The Supplementary Material for this article can be found online at: https://www.ssph-journal.org/articles/10.3389/ijph.2024.1607669/full#supplementary-material
References
1.
Brisson R Furstova J Sokolová L Eriksson C Boniel-Nissim M Badura P . Trends in the Link Between Perceived Social Support and Life Satisfaction in Adolescents (2013/14–2021/22): A Cross-National Study. Int J Public Health (2024) 69:1607283. 10.3389/ijph.2024.1607283
2.
Cosma A Stevens G Martin G Duinhof EL Walsh SD Garcia-Moya I et al Cross-National Time Trends in Adolescent Mental Well-Being From 2002 to 2018 and the Explanatory Role of Schoolwork Pressure. J Adolesc Health (2020) 66(6):S50–8. 10.1016/j.jadohealth.2020.02.010
3.
Chatelan A Rouche M Dzielska A Lebacq T Fismen A Kelly C et al Time Trends in Consumption of Sugar-Sweetened Beverages and Related Socioeconomic Differences Among Adolescents in Eastern Europe: Signs of a Nutrition Transition? Am J Clin Nutr (2021) 114(4):1476–85. 10.1093/ajcn/nqab175
4.
Ottová-Jordan V Smith O Gobina I Mazur J Augustine L Cavallo F et al Trends in Multiple Recurrent Health Complaints in 15-Year-Olds in 35 Countries in Europe, North America and Israel From 1994 to 2010. Eur J Public Health (2015) 25:24–7. 10.1093/eurpub/ckv015
5.
Honkala S Vereecken C Niclasen B Honkala E . Trends in Toothbrushing in 20 Countries/Regions From 1994 to 2010. Eur J Public Health (2015) 25:20–3. 10.1093/eurpub/ckv013
6.
Boniel-Nissim M Lenzi M Zsiros E de Matos M Gommans R Harel-Fisch Y et al International Trends in Electronic Media Communication Among 11-to 15-Year-Olds in 30 Countries From 2002 to 2010: Association With Ease of Communication With Friends of the Opposite Sex. Eur J Public Health (2015) 25:41–5. 10.1093/eurpub/ckv025
7.
Schnohr CW Molcho M Rasmussen M Samdal O de Looze M Levin K et al Trend Analyses in the Health Behaviour in School-Aged Children Study: Methodological Considerations and Recommendations. Eur J Public Health (2015) 25(Suppl. l_2):7–12. 10.1093/eurpub/ckv010
8.
Roberts C Currie C Samdal O Currie D Smith R Maes L . Measuring the Health and Health Behaviours of Adolescents Through Cross-National Survey Research: Recent Developments in the Health Behaviour in School-Aged Children (HBSC) Study. J Public Health (2007) 15(3):179–86. 10.1007/s10389-007-0100-x
9.
Roberts C Freeman J Samdal O Schnohr CW de Looze ME Nic GS et al The Health Behaviour in School-Aged Children (HBSC) Study: Methodological Developments and Current Tensions. Int J Public Health (2009) 54(2):140–50. 10.1007/s00038-009-5405-9
10.
Schmidt-Catran AW Fairbrother M . The Random Effects in Multilevel Models: Getting Them Wrong and Getting Them Right. Eur Sociol Rev (2016) 32(1):23–38. 10.1093/esr/jcv090
11.
Zaborskis A Kavaliauskiene A Levi S Tesler R Dimitrova E . Adolescent Toothbrushing and Its Association With Sociodemographic Factors-Time Trends From 1994 to 2018 in Twenty Countries. Healthcare (2023) 11(24):3148. 10.3390/healthcare11243148
12.
R Core Team. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing (2024). Available from: https://www.R-project.org/ (Accessed October 19, 2024).
13.
Bates D Mächler M Bolker B Walker S . Fitting Linear Mixed-Effects Models Using lme4. J Stat Softw (2015) 67(1):1–48. 10.18637/jss.v067.i01
14.
Giner G Smyth GK . Statmod: Probability Calculations for the Inverse Gaussian Distribution. R J (2016) 8(1):339–51. 10.32614/rj-2016-024
15.
Dunn PK Smyth GK . Generalized Linear Models With Examples in R. Springer Texts in Statistics. New York, NY: Springer (2018). Available from: http://link.springer.com/10.1007/978-1-4419-0118-7 (Accessed October 19, 2024).
16.
Lüdecke LD . ggeffects: Tidy Data Frames of Marginal Effects From Regression Models. J Open Source Softw (2018) 3(26):772. 10.21105/joss.00772
17.
Lüdecke D . sjPlot: Data Visualization for Statistics in Social Science (2024). Available from: https://CRAN.R-project.org/package=sjPlot (Accessed October 19, 2024).
18.
Bryan ML Jenkins SP . Multilevel Modelling of Country Effects: A Cautionary Tale. Eur Sociol Rev (2016) 32(1):3–22. 10.1093/esr/jcv059
19.
Stegmueller D . How Many Countries for Multilevel Modeling? A Comparison of Frequentist and Bayesian Approaches. Am J Polit Sci (2013) 57(3):748–61. 10.1111/ajps.12001
20.
Wood SN . Generalized Additive Models: An Introduction with R. 2nd ed.Boca Raton London New York: Chapman and Hall/CRC (2017). p. 476.
21.
de Looze ME Henking C Torsheim T Currie DB Weber MW Aleman-Diaz AY . The Association Between MPOWER Tobacco Control Policies and Adolescent Smoking Across 36 Countries: An Ecological Study Over Time (2006–2014). Int J Drug Policy (2022) 109:103871. 10.1016/j.drugpo.2022.103871
22.
Fairbrother M . Two Multilevel Modeling Techniques for Analyzing Comparative Longitudinal Survey Datasets*. Polit Sci Res Methods (2014) 2(1):119–40. 10.1017/psrm.2013.24
Summary
Keywords
HBSC study, trend analysis, methodological research, comparative analyses, toothbrushing
Citation
Torsheim T, Elgar FJ, Cosma A, Residori C, Samdal O and Schnohr C (2025) Methodological Approaches to Comparative Trend Analyses: The Case of Adolescent Toothbrushing. Int J Public Health 69:1607669. doi: 10.3389/ijph.2024.1607669
Received
18 June 2024
Accepted
18 December 2024
Published
10 January 2025
Volume
69 - 2025
Edited by
Andrea Madarasova Geckova, University of Pavol Jozef Šafárik, Slovakia
Reviewed by
Eva Cantoni, University of Geneva, Switzerland
Kastytis Šmigelskas, Lithuanian University of Health Sciences, Lithuania
Updates
Copyright
© 2025 Torsheim, Elgar, Cosma, Residori, Samdal and Schnohr.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Torbjørn Torsheim, torbjoern.torsheim@uib.no
This Original Article is part of the IJPH Special Issue “Trends in Adolescent Health and Wellbeing - 40 Years of the HBSC Study”
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.